χ² testy
Chí kvadrát test dobrej zhody – pre jednu kategoriálnu premennú
- zisťujeme, ako veľmi sa líšia namerané početnosti od očakávaných
Postup pri riešení – test dobrej zhody
- Stanovíme si H0 a H1 (IBA slovne)
- Stanovíme si hladinu významnosti α
- Vypočítame si očakávané hodnoty: pravdepodobnosť . komplet súčet meraní
- Overíme si podmienku, že mi je viac alebo rovné 5 (VŠETKY premenné!)
- Stanovíme si stupeň voľnosti DF: k – 1 (k označuje počet kategórii)
- Vypočítame si chi-kvadrát
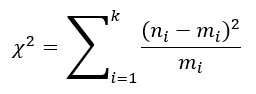
- Nakreslíme si obrázok chi rozdelenia a odhadom označime, kde si myslíme, že sa vypočítané chi nachádza
- Zvýrazníme si graf od bodu chi-kvadrátu do prava = p hodnota
- Vypočítame p hodnotu v exceli: CHISQ.DIST.RT(𝑥2;DF)
- Porovnáme p hodnotu a α hodnotu
- Ak je p hodnota väčšia: Nemôžeme zamietnúť H0
- Ak je p hodnota menšia: Zamietame hypotézu H0 v prospech H1
Dôležité poznámky!
Ak sa skutočnosť rovná očakávaniam tak 𝑥2 = 0 (minimálna hodnota akú 𝑥2 môže mať)
Chí kvadrát test nezávislosti – pre dve kategoriálne premenné
- zisťujeme, či sú kategórie nezávislé od seba, alebo či na sebe závisia
Postup pri riešení – test nezávislosti
- Stanovíme si H0 a H1 (IBA slovne)
- Stanovíme si hladinu významnosti α
- Spravíme si tabuľku skutočných hodnôt
- Vypočítame očakávané hodnoty pre každý vzorcom (súčin súčtu meraní v riadku a súčtu meraní v stĺpci, vydelený s kompletným súčtom meraní)
- Overíme si podmienku, že mi je viac alebo rovné 5 (VŠETKY premenné!)
- Stanovíme si stupeň voľnosti DF: k – 1 (pozor! každú premennú treba zvlášť vyrátať a následne ich vynásobíme: r – 1 . s – 1)
- Vypočítame si chi-kvadrát
- Nakreslíme si obrázok chi rozdelenia a odhadom označime, kde si myslíme, že sa vypočítané chi nachádza
- Zvýrazníme si graf od bodu chi-kvadrátu do prava = p hodnota
- Vypočítame p hodnotu v exceli: =CHISQ.DIST.RT(𝑥2;DF) Poznámka: DF=(r-1).(s-1)
- Porovnáme p hodnotu a α hodnotu
- Ak je p hodnota väčšia: Nemôžeme zamietnúť H0
- Ak je p hodnota menšia: Zamietame hypotézu H0 v prospech H1
Testovanie hypotéz – T-rozdelenie
Čo ak nie sú splnené podmienky?
Opäť zbierame dôkazy na to, aby sme zamietli H0, lenže jedna podmienka (n>30) nie je splnená.
Pri t-rozdelení vyzerá krivka grafu veľmi podobne ako Gaussova krivka, akurát je nižšia a širšia, jej tvar totižto závisí od stupňov voľnosti DF, ktorý zase závisí od počtu ľudí vo vzorke
Postup pri riešení cez interval spoľahlivosti
- Čo poznáme? Poznáme n? Poznáme x? Poznáme s?
- Stanovíme si H0 a H1 (aj matematicky)
- Overíme centrálnu limitnú teorému (CLT)
- Obsahuje vzorka náhodné premenné?
- Je 10% populácie VIAC ako n?
- Je n viac ako 30?
- Ak podmienka 3 z CLT nie je splnená vyriešime problém cez t-rozdelenie
- Stanovíme si hladinu významnosti α, ktorá bude slúžiť aj ako pravdepodobnosť
- Vypočítame si smerodajnú chybu SE
- Nakreslíme si obrázok t-rozdelenia s intervalom spoľahlivosti, kde stredom je očakávaná hodnota
- Určíme si hodnotu stupňov voľnosti DF (k – 1)
- Vypočítame si t-skóre excelom: =T.INV.2T(pravdepodobnosť;DF)
- Použijeme vzorec pre ľavú a pravú hranicu intervalu spoľahlivosti:
- ĽH: x – t-skóre . SE
- PH: x + t-skóre . SE
- Výsledok napíšeme vo formáte: μ ⋲ <ĽH;PH>
Dôležité poznámky: vzorce
na ľavý chvostík grafu pri t-rozdelení: =T.DIST(t-scóre;DF;TRUE)
na pravý chvostík grafu pri t-rozdelení: =T.DIST.2T(t-scóre;DF;TRUE)
pre oba chvostíky grafu pri t-rozdelení: =T.DIST.RT(t-scóre;DF;TRUE)
ak poznáme pravdepodobnosť pri t-rozdelení: =T.INV() alebo T.INV.2T()
Postup pri riešení cez p hodnotu tzv. T-TEST
- Čo poznáme? Poznáme n? Poznáme x? Poznáme s?
- Stanovíme si H0 a H1 (aj matematicky)
- Overíme centrálnu limitnú teorému (CLT)
- Obsahuje vzorka náhodné premenné?
- Je 10% populácie VIAC ako n?
- Je n viac ako 30?
- Ak podmienka 3 z CLT nie je splnená vyriešime problém cez t-rozdelenie
- Stanovíme si hladinu významnosti α
- Vypočítame si smerodajnú chybu SE – štatistika, ktorou meriame skutočnosť od odhadu, vzorcom
- Vypočítame si t-skóre vzorcom (vzorec je rovnaký ako na z-skóre
- Nakreslíme si obrázok t-rozdelenia s intervalom spoľahlivosti, kde stredom je očakávaná hodnota
- Určíme si hodnotu stupňov voľnosti DF (k – 1)
- Dosadíme si hodnoty do vzorca a vypočítame: p hodnota = P (| t | > t-scóre)
- Vypočítame v exceli: =T.DIST.2T(t-scóre;DF)
