- pomocou vzorky vieme vytvoriť tvrdenie o populácii
| parametre (pri populácii) | opisné štatistiky (pri vzorke) | |
| priemer | μ | x̄ |
| smerodajná odchýlka | σ | S |
| relatívna početnosť | p | 𝑝̂ |
Zaujímavé fakty:
Čím je vzorka väčšia, tým je SE menšia.
Čím je interval spolahlivosti väčší (širší), tým sme si viac istý
Postup pri odhade parametra:
1. Čo poznáme (poznáme n?, p?, x?, s?)
- Čo poznáme (poznáme n? poznáme p? poznáme x? poznáme s?)
- Určíme bodový odhad = odhad parametra populácie za pomoci opisnej štatistiky vzorky
- Overíme centrálnu limitnú teorému (CLT)
- Pre relatívnu početnosť:
- Obsahuje vzorka náhodné premenné?
- Je 10% populácie VIAC ako n?
- Je n . 𝑝̂ viac ako 10?
- Je n . (1 – 𝑝̂) viac ako 10
- Pre priemer
- Obsahuje vzorka náhodné premenné?
- Je 10% populácie VIAC ako n?
- Je n viac ako 30?
- Pre relatívnu početnosť:
- Vypočítame si smerodajnú chybu – štatistika, ktorou meriame skutočnosť od odhadu
pre relatívnu početnosť:
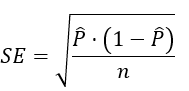
pre priemer:

- Nakreslíme si normálne rozdelenie, do stredu si dáme bodový odhad a vyznačíme si interval spoľahlivosti
- Z scóre býva pre tieto intervaly takéto:
- 90% z = 1,64
- 95% z = 1,96
- 99% z = 2,58
- Použijeme vzorce pre ľavú a pravú hranicu intervalu spoľahlivosti:
- ĽH=p(x) – z . SE
- PH=p(x) + z . SE
alternatívny vzorec:
ĽH: bodový odhad (p/x) – tolerancia chyby ME
PH: bodový odhad (p/x) + tolerancia chyby ME
- Výsledok napíšeme vo formáte:
- Pre relatívnu početnosť: p ⋲ <ĽH;PH>
- Pre priemer: μ ⋲ <ĽH;PH>
- Poznámky „navyše“: tolerancia chyby ME = z-skóre . smerodajná chyba SE (ME = z . SE
